Ποιό είναι το πρώτο πράγμα που σκέφτεστε αφού αγοράσετε ένα δώρο για ένα φίλο, σύντροφο, συγγενή ή συνεργάτη; Μα φυσικά, το περιτύλιγμά του! Μπορεί να μη του δίνουμε τόση σημασία αλλά είναι αυτό που αφήνει την πρώτη εντύπωση και αυτό με το οποίο γίνεται η πρώτη επαφή του παραλήπτη, προτού ανοίξει και αντικρύσει το δώρο του.
Ποιές είναι οι επιλογές σας, λοιπόν;
α) Να σας το τυλίξει ο υπάλληλος του καταστήματος απ’όπου το αγοράσατε.
β) Να πάτε το δώρο (αν το έχετε φτιάξει εσείς ή είναι κάτι ήδη υπάρχον) σε ένα μαγαζί ώστε να σας το τυλίξουν.
γ) Να το τυλίξετε εσείς οι ίδιοι.
Όσοι επιλέξετε το (γ), πολύ καλώς κάνατε! Το τύλιγμα από εσάς τους ίδιους αφ’ενός δίνει άλλη αξία στο δώρο, αφ’ετέρου θα ταιριάζει περισσότερο στα γούστα σας αλλά και τα γούστα του παραλήπτη, αφού μπορείτε να το κάνετε όπως ακριβώς θέλετε. Και εδώ έρχεται το ερώτημα: Πως τυλίγουμε ένα δώρο και πόσο χαρτί χρειαζόμαστε;
Στην προσπάθεια αυτή συχνά σπαταλάμε χαρτί και χρόνο, με αμφίβολο αποτέλεσμα. Υπάρχει, όμως, ένας απλός μαθηματικός τύπος που θα σας λύσει τα χέρια!
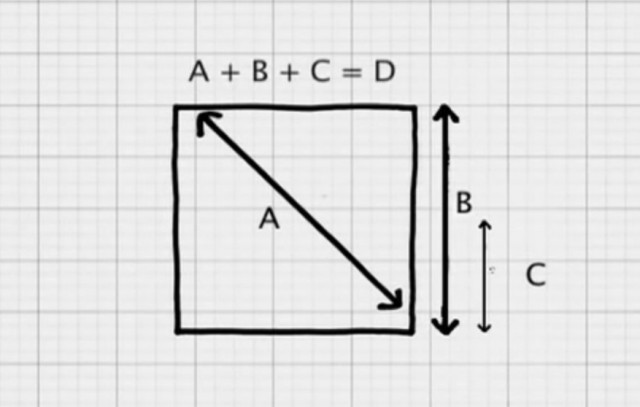
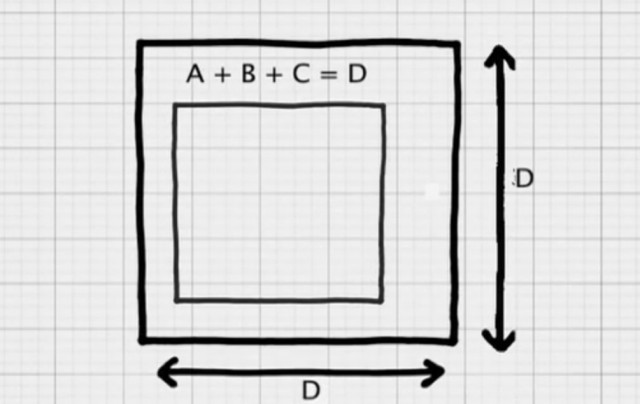
Υποθέτοντας ότι πρόκειται για ένα τετράγωνο ή ορθογώνιο κουτί που περιέχει το δώρο, αρχικά μετράτε τη διαγώνιό του και την προσθέτετε στο ΥΨΟΣ του επί 1,5 φορά.
Στη συνέχεια, κόβετε ένα κομμάτι χαρτί περιτυλίγματος που θα είναι τετράγωνο, με μήκος πλευράς το παραπάνω άθροισμα. Τοποθετείτε το κουτί σε γωνία 45 μοιρών στο χαρτί, αναδιπλώνετε τις 4 πλευρές, σελοτέιπ ή/και ένα φιόγκο και είστε έτοιμοι, έχοντας καταναλώσει το ελάχιστο δυνατό χαρτί!
— Η κατηγορία XMAS 2014 του digitalife.gr περιλαμβάνει gadgets και λοιπά θέματα και αφιερώματα με αφορμή την εορταστική περίοδο των Χριστουγέννων. Περισσότερα ωστόσο για τις Χριστουγεννιάτικες αγορές σας μπορείτε να βρίσκετε στο θεματικό χριστουγεννιάτικο site της Smart Press www.xmaslife.gr. —







τα σχόλια είναι κλειδωμένα.