Το Google Search μάς εκπλήσσει και πάλι… Η νέα “τρισδιάστατη” δυνατότητά του που θα σε κάνει να κολλήσεις

Η μηχανή αναζήτησης της Google πρωτοπορεί για ακόμη μία φορά…

Τώρα και με 3D γραφήματα!

Η νέα δυνατότητα σας επιτρέπει πληκτρολογώντας συναρτήσεις στο Google Search να βλέπετε υπέροχα δυναμικά τρισδιάστατα γραφήματα.

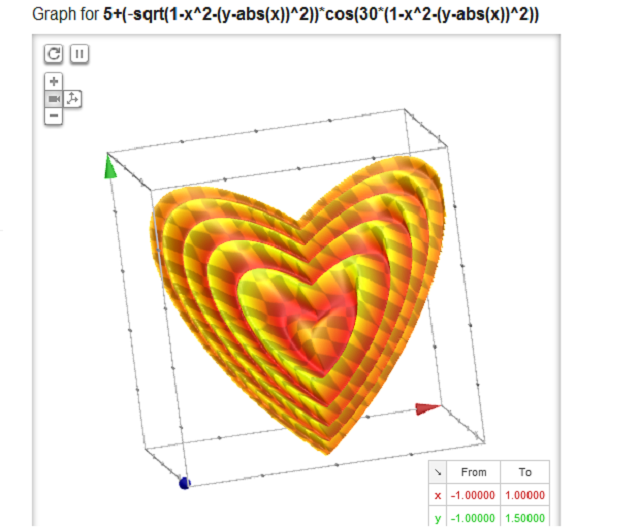
Για παράδειγμα, αν βάλετε στο πεδίο αναζήτησης το “5 + (-sqrt(1-x^2-(y-abs(x))^2))*cos(30*((1-x^2-(y-abs(x))^2))), x is from -1 to 1” θα έχετε μία τρισδιάστατη… καρδιά. Δοκιμάστε το!

Μπορείτε να κάνετε πολλές δοκιμές, με συναρτήσεις που κυκλοφορούν ήδη στο Internet (να μία ακόμη: “sqrt(x*x+y*y)+3*cos(sqrt(x*x+y*y))+5“), ώστε να απολαύσετε το νέο χαρακτηριστικό της Google.

Το γράφημα που προκύπτει μπορείτε να το περιστρέψετε με το ποντίκι σας ή πατώντας το πλήκτρο “Play” στο παράθυρό του. Μπορείτε ακόμη να κάνετε zoom και να δείτε λεπτομέρειες για τους άξονες X, Y και Ζ.

Η νέα λειτουργία, όπως αναφέρει η Google, είναι, προς το παρόν, διαθέσιμη για Chrome και Firefox, δύο browsers που υποστηρίζουν WebGL hardware accelaration και όχι για Microsoft Internet Explorer.

BONUS: Αν σας άρεσε η λειτουργία, δοκιμάστε μερικές ακόμη συναρτήσεις

1/(sin(abs(x)+x)-cos(abs(y)+y))
sin(5.5x)*cos(5*y)+x*x+1
5000-140*(x*x+y*y)+(x*x+y*y)^2
sin(x^2+y^2)/(abs(x*y)+1) from -2.5 to 2.5
tanh(y(y^4+5x^4-10(x^2)(y^2))/(x^2+y^2)^4)
(x^2+((3 y)/2-(x^2+abs(x)-6)/(x^2+abs(x)+2))^2)-36
sin(5.5x)*cos(5*y)+x*x+1 x is from -1 to 1, y is from -1 to 1, z is from 0.1 to 2.8
100-3/(sqrt(x^2+y^2))+sin(sqrt(x^2+y^2)), x is from -10 to 10, y is from -10 to 10, z is from 85 to 101
5 + (-sqrt(1-x^2-(y-abs(x))^2))*cos(30*((1-x^2-(y-abs(x))^2))), x is from -1 to 1, y is from -1 to 1.5, z is from 1 to 6
100-3/(sqrt(x^2+y^2))+sin(sqrt(x^2+y^2))+sqrt(200-(x^2+y^2)+10*sin(x)+10sin(y))/1000, x is from -15 to 15, y is from -15 to 15, z is from 90 to 101
sqrt(x*x+y*y)+50*tan(sqrt(x*x+y*y))
exp(-((x-4)^2+(y-4)^2)^2/1000) + exp(-((x+4)^2+(y+4)^2)^2/1000) + 0.1exp(-((x+4)^2+(y+4)^2)^2)+0.1exp(-((x-4)^2+(y-4)^2)^2)
sqrt(cos(3*x))*cos(100*y)+1.5*sqrt(abs(x)) + 0.8 x is from -1 to 1, y is from -1 to 1, z is from 0.01 to 2.5
sqrt(x*y+y*y)+3*sin(sqrt(x*x+y*y))+5 from -20 to 20
sqrt(x*x+y*y)+3*tan(sqrt(x*x+y*y))+10
x^2+y^2+x*y*sin(x+y) from -20 to 20

Πηγές: Mashable, WebGL